Abstract : The simulation of different types of trapped particles and the comparison with theoretical values is accomplished . It is a previous step to allow satisfactory results with the module to simulate collisions and their effects. Boozer-like coordinates is a kind of reference of each point on each magnetic surface to an origin which is the x+ axis. It obtains correct graphical results but differs from the concept of Boozer coordintes. In general all the results agree with theory but further test is convenient.
About poloidal projections and Boozer
First simulations of banana orbits in tokamaks and stellarators were carried out in [1]. In tokamaks the representation was correct but in stellarators the process was manual and inaccurate.
A more perfect method is necessary to know what is happening in a "Plasma" composed by, for example, 300 or 1000 quasi-particles (1016 to 1019 m-3) with trapped, untrapped, trapping-detrapping, n = f(r) , maxwellian distribution of speeds, electrons and ions...
A first try of simulation of 20 plasmas of different densities with collisionality from P-S to collisionless has been recently achieved but the results are confusing. So the analysis of the behaviour of individual particles is necessary.
Geometrical representation of poloidal projections of trajectories is inadequate in UST_1 (and in general in stellarators) as can be observed in Figure 5. The superior part is the effect of throwing a proton in co (red) and counter (cyan) B direction. The different drift orbits are barely observed because the loops difficult the vision and no measures can be done on the graph.
Some effort was done to obtain a useful method of Boozer style representation. Boozer coordinates are not adequate for the philosophy of SimPIMF so it can only act as representation method and/or to express initial conditions. Moreover it seemed time consuming the implementation of correct Boozer coordinates. So a Boozer-like method is used.
Boozer-like coodinates
A new module is developed to transform each 3D point, P, in a 2D, Q, adequate point. The method is :
An orbit in reversed sense (Vparallel <0) is started from P till the orbit pass very near the x+ axis, R point, and rough R' point. The distance from R to the magnetic axis is stored, r . Iota is calculated for the surface that contain R (it could be stored and interpolated to speed up the code). From R' point to P the toroidal angle is known. Toroidal * Itoa = resulting poloidal Boozer like angle of Q. Toroidal angle is set to 0 . r is taken instead of radial Ψ coordinate of Q. Flux and J do not participate.
Some cases of trapped
particles in UST_1
Helically trapped
Figure 1. In magenta the poloidal projection in Boozer-like coordinates of the trajectory of an electron with initial Vt_Ratio =0.3 ( projection on B for unitarian speed). Ecin = 10eV . Magnetic field corresponding to 1st harmonic ECH = -4400 A-turn (~twice the present real value). Life of particle 7.7 microsec. It is a helically trapped particle, not modular ripple trapped because it oscillates about 90º toroidal degrees.
In blue (almost black) the circular centred passing orbit (without drifts, type 'P').
UST_1 tend to produce ripple trapped particles if the case is not carefully studied. This case was obtained after some analysis of the distribution of B on magnetic field lines [2] and two tries.
A mod-B plot of a magnetic surface would be useful but is not available by now.
The drift speed in the simulation fulfil the analytical calculation. Most of the theoretical information cames from U. Stroth [3] and Dolan.
Modular ripple trapped
Figure 2 . In green an electron thrown from a more external surface than in Figure 1. Electron with initial Vt_Ratio =0.15 . Ecin = 10eV . -4400 A-turn , It is a modular trapped electron, not a helically trapped because it oscillates ~15º between two modular coils.
In yellow the circular centred passing orbit starting from the same point. Obtained without drifts, type 'P' simulation.
Modular ripple is ~1/2 of the helical ripple in UST_1 so modular ripple trapped particles have a behaviour similar to the helically trapped. They only differs from the toroidal excursion.
The present non-optimised Boozer-like transformation is relatively slow. It lasted 400s to represent the green trajectory. Nearly the same result is obtained with a Step five times larger and then it lasted only 80 seconds.
Banana orbits and pssing orbits
Figure 3 . In green an electron with initial Vt_Ratio =0.45 ini x = mag axis+15mm. Ecin = 10eV . -4400 A-turn. The banana with on the graph is 2.5mm . From expressions : 2.3mm from Dolan pg 164 , ~2.6mm from one expression in [3] and 1.3 from another expression in [3]. It is not clear why one expresion gives different result. It will be recalculated if more expressions are available. In yellow the passing non-drifts orbit ('P' simulation)
Figure 4
Two passing orbits simulated with 'D' simulation (with drifts), thrown from the same point as the trapped electron, at Vt_Ratio = +-0.6. The co-orbit (with respect B direction) in cyan and the counter in magenta.
In yellow the passing non-drifts orbit ('P' simulation)
The simulation lasted 122s using large "Step" (0.5 ns , nanoseconds)
An anomaly remains in the representation that seems a kind of jump in the poloidal values (see magenta line in Figure 4)
Necessary improvements and tests
The anomaly in the representation should be corrected . Calculate the theoretical banana width with new expressions.
References
[1] " Simulation of banana orbits in tokamaks and stellarators" Vicente M. Queral. See All past research
[2] "Simulations in UST_1. Magnetic surfaces, islands, Iota and Magnetic Well profiles". Vicente M. Queral. See All past research
[3] " 9 Transport in Toroidal Plasmas" U. Stroth
Figure 1 . Simulation of helically trapped electron represented in Boozer-like coordinates. The particle has Vt_Ratio =0.3 ( projection on B for unitarian speed). Ec = 10eV . -4400 A-turn . Life of particle 7.7 microsec. It is a helically trapped particle, not modular ripple trapped, about 90º toroidal oscillation.
Figure 1 . Simulation of helically trapped electron represented in Boozer-like coordinates. The particle has Vt_Ratio =0.3 ( projection on B for unitarian speed). Ec = 10eV . -4400 A-turn . Life of particle 7.7 microsec. It is a helically trapped particle, not modular ripple trapped, about 90º toroidal oscillation.
Figure 2. Simulation of modular ripple trapped electron represented in Boozer-like coordinates. The particle has Vt_Ratio =0.15 ( projection on B for unitarian speed). Ec = 10eV . -4400 A-turn . It is a modular trapped electron, not a helically trapped because it oscillates ~15º between two modular coils.
Figure 3. Simulation of banana orbit in UST_1
Figure 4. Banana orbit together with pasing orbits. The co-orbit (with respect B direction) in cyan and the counter in magenta. In yellow the passing non-drifts orbit
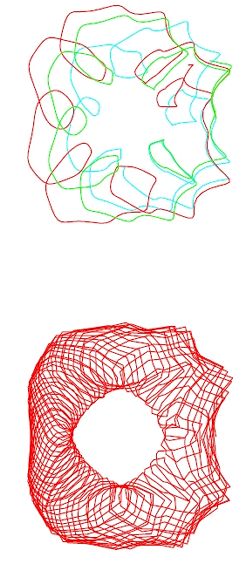
Figure 5 . Useless geometrical representation of poloidal projections in UST_1 . The superior part is the effect of throwing a proton in co (red) and counter (cyan) B direction. The projections are confusing
Date of publication 23-10-2006.