Abstract : The simulation of the magnetic surfaces at 3 toroidal angles is carried out. Islands are obtained and analysed resulting that only relatively low rationals remain in the plasma region. Iota profile is decreasing and moderately flat, so shear is enough but the rational 2/7 falls inside the plasma. There is a magnetic well of 2% at edge. Root-mean-square error of |B|min was optimised by a factor of two with respect the 'natural' case, however excessive modular ripple exists due to low number of coils.
Reason for new simulations
No previous simulations were run for exactly the real built UST_1. For example the ones in [1] , [2] and [3] correspond to previous designs and not to the definitive UST_1. Moreover this data is necessary to carry out simulations of trapped particles and collisions.
Vacuum magnetic surfaces in UST_1
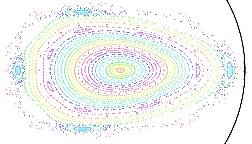
SimPIMF is run in 'P' = Poincaré simulation to obtain the magnetic surfaces on 3 different toroidal angles. Intersections for toroidal 0º, 45º and 90º are calculated because it is a m=2 stellarator.
The results are shown in Fig. 1 Fig. 2 and Fig. 3 . A new process is used for the representation by printing to a pdf file.
x axis is taken as the reference to throw particles. The step between particles is 1mm towads x+ from the magnetic axis. 33 particles give numerous turns so many intersection points. Particles more external than nº33 escape after 1 or few turns.
The common stochastic region is formed. Here only the two external orbits are stochastic. In the 'natural' non-optimised case many external orbits were non-confining.
The improvement with respect non-optimised cases shown in [1] is notable.
Figure 4. Islands
Island independent of the x axis (do not cross the axis at x+) are not obtained automatically and need to be obtained manually. A particle is thrown in the probable point and the of islands appear. This is done in Figure 4 to obtain the 4 remaining 1/4 islands, the remaining 10 of the 3/10 rational, and others . The 'Grid' is set to 1/200m in this case to obtain larger islands due to increase of magnetic perturbations.
Islands from right to left in Fig. 4:
In blue : 1/4 = 2/8
No visible : 3/11, 4/15 ….
Magenta : 2/7 . The island is not very small, but acceptable in UST_1.
Size of island should be proportional to (Berror/ m * Shear)^0.5
, rational n/m
Green : 3/10 = 6/20
Magenta : 4/13
No visible, green : 5/16
The accuracy in the calculation of Iota values is high using only 49 seconds per surface :
Values of Iota,
Blue : 1/4 . Calculated = 0.2500315
Magenta : 2/7 = 0.28571 , calculated = 0.2856076
Green : 3/10 . Calculated 0.2999538
Iota and Magnetic Well profiles
An accurate simulation to obtain Iota profile is performed. Rough profiles are calculated in 90s but this figure lasted 1960 seconds to obtain the minimum errors (similar to the ones in "Values Iota" above)
A small perturbation can be seen in Figure 5 at x=21 x=22 due to the island 2/7 .
Iota profile is tokamak like because a crescent one (W7-X and other) was not obtained by the SimPIMF optimization process.
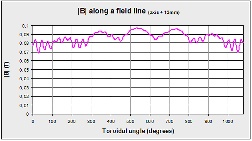
B along field lines
Figure 7 shows |B|min for UST_1 on a surface x=13mm. The root-mean-square error of |B|min on a surface x=15mm was optimised with SimPIMF during the design. The 'natural' non optimised case (1.25 1.25 1.25 1.25 parameters of shape) has δ = 0.0061 and UST_1 δ= 0.0038. The optimization is notable, even more considering that plasma size and other 5 parameters were weighted simultaneously.
An important modular ripple is observed. This ripple is caused by the finite number of modular coils. It is important because only 12 TF coils (6 per period) form UST_1 . However Garabedian [4] [5] and Najmabadi [6] seems to calculate good quality stellarators with 12 modular coils and m=2 (similar to UST_1). Clearly they optimise the coils in free 3D surfaces and by means of very powerful codes.
No averages of δ of |B|min in the plasma volume are calculated or optimised.
Plasma size and Aspect Ratio
Plasma size has been calculated. The area enclosed in the last closed magnetic surface on 3 poloidal cross sections is measured. The Plasma size of UST_1 is 1060 cm3 ~ 1.1Litres ~ 1 Litre. The average minor radius of the plasma size is <a> = 20.8mm ~ 20mm . The major radius is Ro =125mm , so the aspect ratio is by chance 6.0096 ~ A = 6
References
[1] "Optimization of Iota, Iota profile, plasma size, Bmin and magnetic well" . Vicente M. Queral. See All past research
[2] " Magnetic surfaces from the improved SimPIMF v1.2 . Calculation of rotational transforms" Vicente M. Queral. See All past research
[3] " Simulation of banana orbits in tokamaks and stellarators" Vicente M. Queral. See All past research
[5] "A TWO FIELD PERIOD CANDIDATE FOR ARIES-CS" P.R. Garabedian. Web
[5] "Compact stellarators with modular coils". Garabedian, PNAS , July 18, 2000 , vol. 97 , no. 15
[6] "Exploration of Compact Stellarators as Power Plants" Farrokh Najmabadi , 16th ANS TOFE
Figure 1 . Vacuum magnetic surface in UST_1 at Φ = 0º .
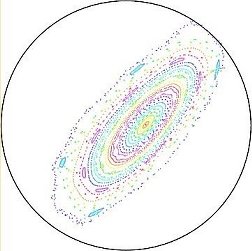
Figure 2 . Vacuum magnetic surfaces in UST_1 at Φ = 45º .
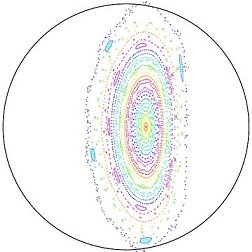
Figure 3 . Vacuum magnetic surfaces in UST_1 at Φ = 90º .
Figure 4 . Simulation of all the visible islands. Low resolution 'Grid' is used to increase the magnetic filed errors and so increase the size of the islands
Figure 5. Iota profile in UST_1 for Beta=0. A relatively flat profile was searched and obtained. Low order rational are avoided. Only 2/7 remains as a notable high rational.
Figure 6. Vacuum Magnetic Well Depth profile in UST_1. There is a magnetic well in UST_1
Figure 7. B along a field line. It corresponds to the magentic surface x=13mm. The |B|min root-mean-square error is optimised with respect the 'natural' non optimised case (1.25 1.25 1.25 1.25 parameters of shape)
Date of publication 23-10-2006.