Abstract : Banana orbits and drifts in a tokamak and stellarator are simulated.
Banana orbits
In a tokamak
The simulation of trapped particles by means of SimPIMF v2.1 with minor modifications is carried out .
Because the code works in cartesian coordinates and there is no Boozer transformation of coordinates, the representation of banana orbits for stellarators is difficult. First a tokamak is simulated.
The code can easily generate a tokamak by taking 0 deformation for the modular coils, so they are planar circular coils, and with the addition of a poloidal coil inside the torus to approximate the plasma current. The poloidal coil is modelled as a winding pack that has 20mm of radius of uniform current in a circular section. This is easy to model in the code and it better approximates the effect of the plasma.
The dimensions of the tokamak are the same as in UST_1.
The plasma current was iteratively calculated to obtain magnetic surfaces.
The magnetic axis is obtained. After that the code calculates the poloidal projection by changing the coodinates.
The particle is simulated without drifs and it is represented in cyan in Graph 1 as the poloidal projection. The banana orbit of the toroidally trapped particle is simulated with a grid = 81 x 81 x 37 nodes (in magenta)
Some differences in the calculation of magnetic surfaces were noticed in [1] due to a low number of nodes of the grid. In yellow the same orbit calculated with a grid 21 x 21 x 9 nodes is shown. The difference is notable. A finner grid should be tested.
The banana half-width calculated from Dolan 7E21 gives an order of magnitude which is 0.4mm . From Graph 1 the result is 1.8mm. It is not clear if the discrepance comes from the aproximate expression in Dolan or due to some imperfection in the simulation. It will be further tested.
In a stellarator : UST_1
Due to the difficult with the helical axis and helical magnetic surfices only a manual reconstuction of the banana orbit from a few points is done.
The Design 2m12C-14120712 of UST_1 is simulated. This is similar to the standard design.
The realtion between module of speed and tangential speed is 0.3 to allow the trapping of the particle.
The Graph 2 has been obtained from the trajectory of a toroidally trapped particle. This particle is trapped by the 1/R variation of field in the stellarator. The intersection of the trajectory of a particle without drifts on the planes X=0 (only on y+) and plane Y=0 (x+ x-) is produced. The same intersection is obtained for the trapped particle. The 3 figures are superposed at the point of the magnetic axis. The different points in the 3 figures are reescaled conserving the poloidal angle so as to obtain a circle for the magnetic surfaces. This is similar to a Boozer transformation. There is a lack of points in the graph.
Perhaps a more serious transformation to Boozer coordinates will be implemented. However because all the results in the code lay on the concept "trajectory" (the series of points of the particle) the conversion seems complex.
In Graph 3 the drift of an electron helically trapped is shown.
Some other previous simulations can be seen in [2]
References
[1] "Magnetic surfaces from the improved SimPIMF v1.2 . Calculation of rotational transforms" Vicente M. Queral . See ôList of all past R&D" in this web.
[2] "Simulation of trapped particles for the optimization of UST_1 coils" Vicente M. Queral . See ôList of all past R&D" in this web.
Graph 1. Tokamk. Poloidal projections of the trajectory of one particle.
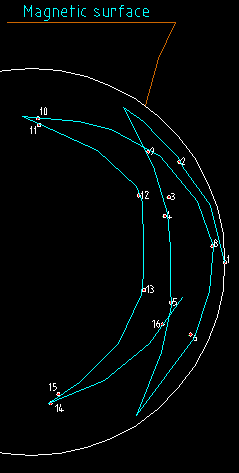
Graph 2. Stellarator. Poloidal projection in a Boozer-like coordenates. The points are obtained manually from the 3D trajectory.
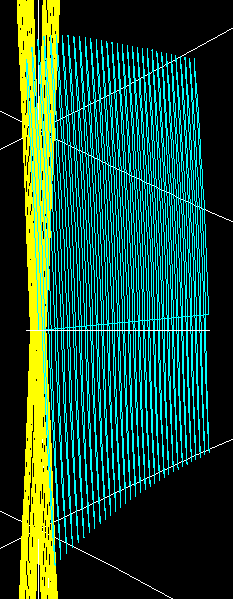
Graph 3 . Trajectories of an helically trapped particle. (The figure is rotated 90║) . In yellow the magnetic axis.
Date of publication 06-03-2005
