Abstract : An initial code for Monte Carlo
simulation of trajectories of plasma particles is developed. Only basic
behaviour of the particles is implemented. The main objective is educative
due to the CPU limitations and because PIC (particle in a cell) algorithms
are not implemented. Only velocity drifts due to B gradient, centrifugal
force and electrical fields are implemented up to the present . No
diamagnetism and magnetic field due to the movement of the particles is
implemented in this version.
General description
Different codes exist to simulate plasma
particles using Monte Carlo methods so this code is intended mainly to
personal educative function. Perhaps it might be useful to calculate
magnetic surfaces, magnetic share, losses of particles, etc, in innovative
geometrical magnetic fields.
The calculations are done following the
explanations in Dolan [1], mainly from chapter 7. Non-relativistic behaviour
is considered and a pack of particles forming a quasiparticle is used. 3D
simulation is produced.
The interval of time per step varies
between 10 and 100 picoseconds and simulations have achieved up to 1000
particles and 1 milisecond. The simulation of higher number of particles
requires some kind of PIC algorithm and this falls out of the objective of
the code.
A file with the necessary data is
created in each run. The file contains useful information of each particle
for each 500-2000 steps. At the moment, the results are : cartesian
velocities, velocity parallel and perpendicular to B, energy and magnetic
moment of each particle. The number of particles lost outside a rectangular
box of volume is also saved. Average values are not calculated yet.
Particles start in a random position,
all have the same T=106 K (non-maxwellian distribution), the
poloidal and toroidal velocities are random values but vertical component is
always zero.
The magnetic field is obtained using
MEMCEI v2.1 code and HT-7U tokamak as an example. However the magnetic field
and size is divided by 10. Values of B are taken each 25mm forming a grid.
The magnetic field at each point is interpolated using trilinear
interpolation. Although a preinterpolation of the values and the use of this
values stored in RAM memory has been tried, only the work with exact
interpolation for each (x,y,z) point has been tested. The use of
preinterpolation seems to produce excessive changes in the gradient of B and
so it was avoided. The preinterpolation method is about 5 times faster than
interpoling each particular point that is obtained
step by step.
Some examples of execution
Simulation A was obtained using
100 quasiparticles each one composed of 108 particles of
identical characteristics. There are 50 quasi-ions and 50 quasi-electrons
running. The simulation follow the properties and input data explained
above. The magnetic field is calculated from the TF coils only, no PF and
plasma current is considered. 106 steps of 10 picosecond are
simulated (a total period of 10 microsecond ). Only 3 ions in blue and 2
electrons in reddish are shown in Graph 1 and Graph 2 . The trajectories of
the electrons are graphically represented with less accuracy than ions to
decrease memory consumption. The end of each trajectory appears as a
straight line towards the origin.
The different types of trajectories
observed for ions are caused by the different parallel/perpendicular B
ratios of velocities. Additionally the higher magnetic field at lower major
radius and the higher electric field at equatorial points also influence on
the different trajectories.
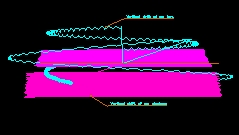
No electrical equilibrium is considered
so electrons drift freely toward decreasing Z values (down in the Graph 1)
and ions follow Z+ paths. This can be observed in Graph 1. With this
conditions the electric field increases continuously and produce a radial
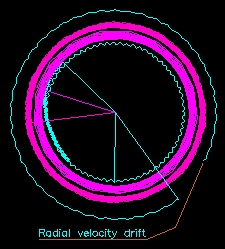
drift of both electrons and electrons that can be seen in Graph 2.
Simulation B tries to
obtain several magnetic surfaces. They are obtained using only one electron.
The magnetic field includes the influence of TF, PF coils and plasma current
at about the instant 13 sec. See [2] and [3] for more information about this
instant. No quasiparticles are utilized. The simulation follow the
properties and input data explained above.
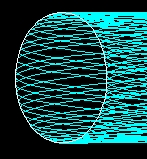
- 3 x 106 steps of 10 picoseconds are simulated in Graph 3 that is a
total period of 30 microsecond . The trajectory of the electron is plotted.
The magnetic surfaced appear clearly defined. The contour of
the magnetic surface is highlighted in white.
Further developments
No further
developments are foreseen. Perhaps the searching of a standard code to
evaluate magnetic field configurations might be useful to select optimum
coil configurations.
References
[1] "Fusion research" T.J. Dolan, Pergamon Press.
[2] "The Analysis and Calculation for the Toroidal Magnetic field of HT-7U" , Chen wenge(陈文革), Pan yannian(潘引年), Wu songtao(武松涛), Weng peide(翁佩德). Institute of Plasma Physics, Chinese Academy of Sciences.
[3] "Profile of the forces on TF coils of HT-7U. Comparison with the results of the HT-7U team" , Vicente M. Queral . See "Present Status" or “Last results”.
Graph 1 . Elevation view of the simulation A
Graph 1 . Elevation view of the simulation A
Graph 2 . Ground plan of the simulation A
Graph 3 . One magnetic surface. Simulation B
Last Update 25-03-2005