Abstract : Calculation of the magnetic surfaces for tilted and for random coils is carried out. The magnetic grid is as fine as possible, limited by the procesing time. The grid is limited to a selected toroidal area to speed up the calculation.
General description
Two series of modified toroidal coils are modelled.
* A) The first series of coils has 6 tilted coils as expressed in
Graph 1. Three cases are analysed: 1) Coils tilted 2.75º , 2) 0.857º and 3)
0.275º
* B) The other set is a random one. The 10 TF coils are randomly
deformed in the toroidal direction. The deformation is a random deviation
from the theoretical circular shape.
The helical coils remain exact.
SimPIMF v1.2 [1] with minor modifications (v1.2.1) is used.
The general process and data is the same as in [1]
Modelling
Three coils are tilted in one direction (in yellow in Graph 1) and the next 3 in the opposite direction (in cyan). The other 4 remain unmodified. The poloidal section presented in the graphs is located between the yellow and cyan coils (0º toroidal).
Case A
1) 2.75º . The result was completely deformed. It is not shown.
2) 0.857º . The conditions are : Grid calculated only at the central torus (using v1.2.1) except the external 2 particles (these points were out of the toroidal grid). Grid of 86 x 86 x 27 nodes. Size of each hexahedron, 10mm. A finest grid takes too long to be calculated with a 3GHz PC. This calculation took about 4 hours. Step time = 1 Nanosecond. The other conditions are like in [1].
The result is shown in Graph 2.
Observations:
* The surfaces are notably shifted downward. The central vertical red line is the vertical shift from the equatorial plane to the magnetic axis. This is similar to the results in [2]. The direction of the shift is obvious from the coil configuration.
* Comparing with Graph 6 (which is the same as Graph 5 in [1] calculated for perfect coils), the external surfaces are deformed and rotated. The 1/3 islands rotate (they will appear clearly with additional perturbations). Something similar also happens in [2].
* The deformation would be unacceptable in a normal stellarator. Moreover it will influence in stability and transport.
* The rotational transform for the green surface formed by 31 small points (the second after the last yellow) is 0.2902 , 0.290337 and 0.290287 for increasing revolutions of the particle. It may be the 9/31 =0,2903225... rational surface. Other surfaces that show discontinuities are also near rational surfaces.
* "Green" surfaces and smaller ones tend to have a drift which seems to be mathematical but not due to the size of the grid. It seems that the asymmetry of this model increases the small mathematical drifts of the algorithm. It will be better analysed and improved.
3) 0.275º . Conditions : Global grid (using v1.2). Grid of 61 x 61 x 25 nodes. Size of each cube, 41.66mm. Graph 3 displays the result. It is much more similar to the one with non-tilted coils. The vertical shift is small, only the central vertical red line. It could be acceptable for a home-made stellarator.
Case B
The coils are deformed on the toroidal surface. The maximum deformation is roughly +-5mm and the speed of the change in the deviation follows a random value that changes 5 times per coil. The diameter of TF coil is 1m. The result is shown in Graph 4.
Conditions : Grid calculated only at the central torus (using v1.2.1). Size of each hexahedron, 10mm. Step time = 1 Nanosecond. The other conditions are like in [1].
Observations :
* The vertical shift is small due to the statistical effect.
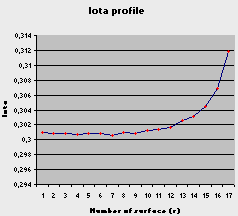
* The rotational transform at the central region is practically flat.
The values of Iota for each particle in Graph 4 are :
| 1 | 0,30077901 |
| 2 | 0,30089301 |
| 3 | 0,30076251 |
| 4 | 0,30085298 |
| 5 | 0,30083733 |
| 6 | 0,30063071 |
| 7 | 0,30095103 |
| 8 | 0,30090236 |
| 9 | 0,30119837 |
| 10 | 0,30144541 |
| 11 | 0,30162674 |
| 12 | 0,3025862 |
| 13 | 0,30308551 |
| 14 | 0,30451398 |
| 15 | 0,30684623 |
| 16 | 0,31180845 |
They are represented in
Graph 5.
Around the centre of the “plasma” the rotational transform is flat
and the value is very near to 0.3 . The reason is
unknown since it does not happen in the exact calculation. The imperfections
in the centre of the Graph 4 are due to the mathematical drift above
mentioned.
Further developments
A tri-quadratic pre-interpoling of the grid would be useful to speed up the calculation process. Mathematical drifts need to be analysed and corrected.
References
[1] "Magnetic surfaces from de improved SimPIMF v1.2 . Calculation of rotational transforms ", Vicente M. Queral . See “Past research"
[2] "Magnetic Filed accuracy and 'Correction' Coils in Wendeltein 7-X" J. Kisslinger adn T Andreeva. Stellarator Workshop 2005.

Graph 1 . Tilted coils. In this case 2.75º.

Graph 2 . Magnetic surfaces for coils tilted 0.857º

Graph 3 . Magnetic surfaces for coils tilted 0.275º
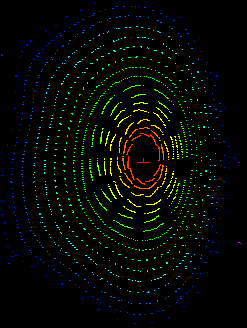
Graph 4 .Magnetic surfaces for aleatorial coils
Graph 5 . Iota profile for aleatorial coils

Graph 6 . Magnetic surfaces related to the Grid 61 x 61 x 25 nodes with perfect coils, See[1].
Last Update 14-11-2005